Рассмотрим обыкновенное дифференциальное уравнение 1–го порядка
Пусть y = y(x) решение уравнения.
Интегральная кривая y = y(x) имеет касательную с угловым коэффициентом k = f(x, y(x)). Это означает, что через каждую точку (x, y) области определения функции f(x, y) можно провести небольшой отрезок с угловым коэффициентом k = f(x, y(x)).
Выполнив такое построение для всех узлов некоторой прямоугольной сетки в области определения правой части уравнения , получим изображение поля направлений.Когда узлы сетки расположены "достаточно часто" поле направлений дает полную картину поведения интегральных кривых.
Метод изоклин — приближенный графический метод решения обыкновенных дифференциальных уравнений 1–го порядка.
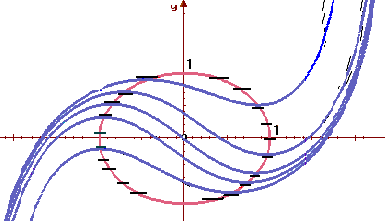
Метод позволяет "вручную" (без использования компьютера) построить изображение поля направлений и по этому изображению построить интегральную кривую, проходящую через заданную точку.Рассмотрим линии, в каждой точке которых угловой коэффициент интегральных кривых имеет одно и то же постоянное значение: f(x, y) = k, k = const.
Такие кривые называются изоклинами дифференциального уравнения y' = f(x, y). Равенство f(x, y) = k — уравнение изоклины.В каждой точке (x, y) изоклины f(x, y) =k интегральные кривые уравнения имеют один и тот же угол наклона ?rctg(?) = k.
Метод изоклин состоит в следующем.Строим достаточно густую сетку изоклин для различнх значений k и на каждой изоклине изображаем небольшие отрезки с наклоном k.
Затем, начиная из точки (x0, y0), поводим линию, которая, будет пересекать каждую изоклину под углом, заданным полем направлений. Полученная таким образом кривая и будет приближенным изображением (эскизом) интегральной кривой уравнения, проходящей через точку (x0, y0).
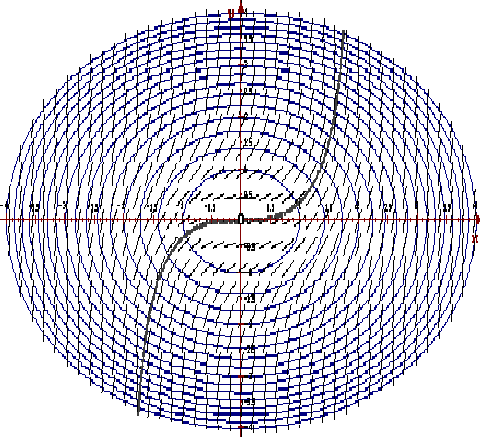
На рисунке изображены изоклины для k = 1,2, … ,15,16 и интегральная кривая, проходящая через точку (0,0) .
Метод изоклин как метод приближенного решения задачи Коши устарел. В его в основе лежит алгоритм изображения фрагмента поля направления, а современные компьютеры могут мгновенно и как угодно подробно нарисовать поле направлений, и достаточно точно изобразить интегральную кривую.
Однако, метод изоклин эффективно работает как инструмент исследования поведения решений. Он позволяет изобразить области характерного поведения интегральных кривых.
Например, изоклина f(x, y) = 0 — геометрическое место стационарных точек решения дифференциального уравнения, изоклины f(x, y) = k с большими значениями k показывают области быстрого роста решений и т.п.
На рисунке показано, как помогают изоклины "увидеть" точки экстремума интегральной кривой и судить о поведении решений дифференциального уравнения.
Метод Эйлера
Рассмотрим дифференциальное уравнение
(1)
с начальным условием
Подставив 
в уравнение (1), получим значение производной в точке 
:
При малом 
имеет место:
Обозначив 
, перепишем последнее равенство в виде:
(2)
Принимая теперь 
за новую исходную точку, точно также получим:
В общем случае будем иметь:
(3)
Это и есть метод Эйлера. Величина 
называется шагом интегрирования. Пользуясь этим методом, мы получаем приближенные значения у , так как производная 
на самом деле не остается постоянной на промежутке длиной 
. Поэтому мы получаем ошибку в определении значения функции у , тем большую, чем больше . Метод Эйлера является простейшим методом численного интегрирования дифференциальных уравнений и систем. Его недостатки – малая точность и систематическое накопление ошибок.
Более точным является модифицированный метод Эйлера или метод Эйлера с пересчетом. Его суть в том, что сначала по формуле (3) находят так называемое «грубое приближение»:
а затем пересчетом 
получают тоже приближенное, но более точное значение:
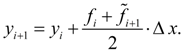(4)
Фактически пересчет позволяет учесть, хоть и приблизительно, изменение производной 
на шаге интегрирования 
, так как учитываются ее значения 
в начале и 
в конце шага (рис. 1), а затем берется их среднее. Метод Эйлера с пересчетом (4) является по существу методом Рунге-Кутта 2-го порядка [2], что станет очевидным из дальнейшего.
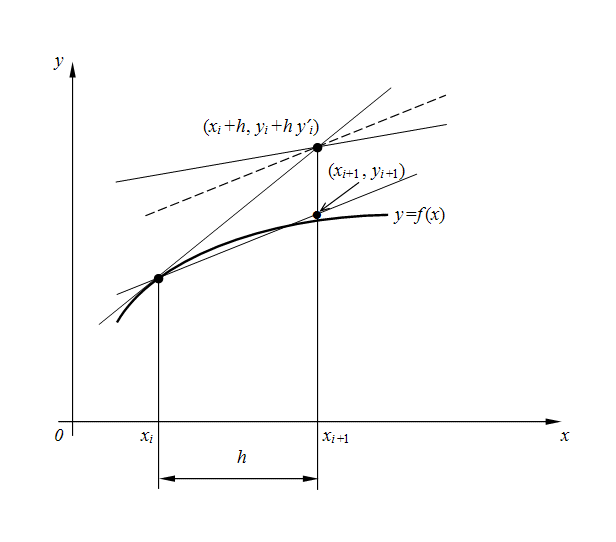
Рис. 1. Геометрическое представление метода Эйлера с пересчетом.
Метод Рунге-Кутта
Вновь рассмотрим дифференциальное уравнение
(1)
с начальным условием 
Классический метод Рунге-Кутта 4-го порядка описывается следующей системой пяти равенств:
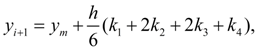(5)
где
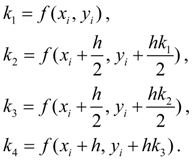
Строго говоря, существует не один, а группа методов Рунге-Кутта, отличающихся друг от друга порядком, т.е. количеством параметров 
. В данном случае мы имеем метод 4-го порядка, который является одним из наиболее применяемых на практике, так как обеспечивает высокую точность и в то же время отличается сравнительной простотой. Поэтому в большинстве случаев он упоминается в литературе просто как «метод Рунге-Кутта» без указания его порядка.
