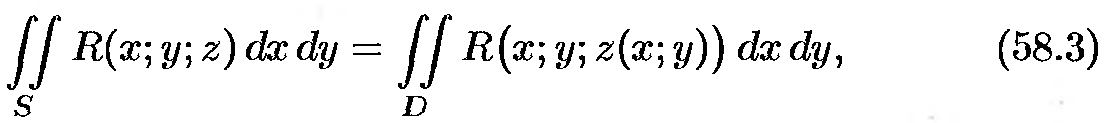27.Поверхностный интеграл II рода.


Основные понятия
Поверхностный интеграл второго рода строится по образцу криволинейного интеграла второго рода, где направленную кривую разлагали на элементы и проектировали их на координатные оси; знак брали в зависимости от того, совпадало ли ее направление с направлением оси или нет
Пусть задана двусторонняя поверхность (любая поверхность задаваемся уравнением

функции, непрерывные в некоторой области D
плоскости Оху)

после обхода такой поверхности, не пересекая ее границы, направление нормали к ней не меняется.
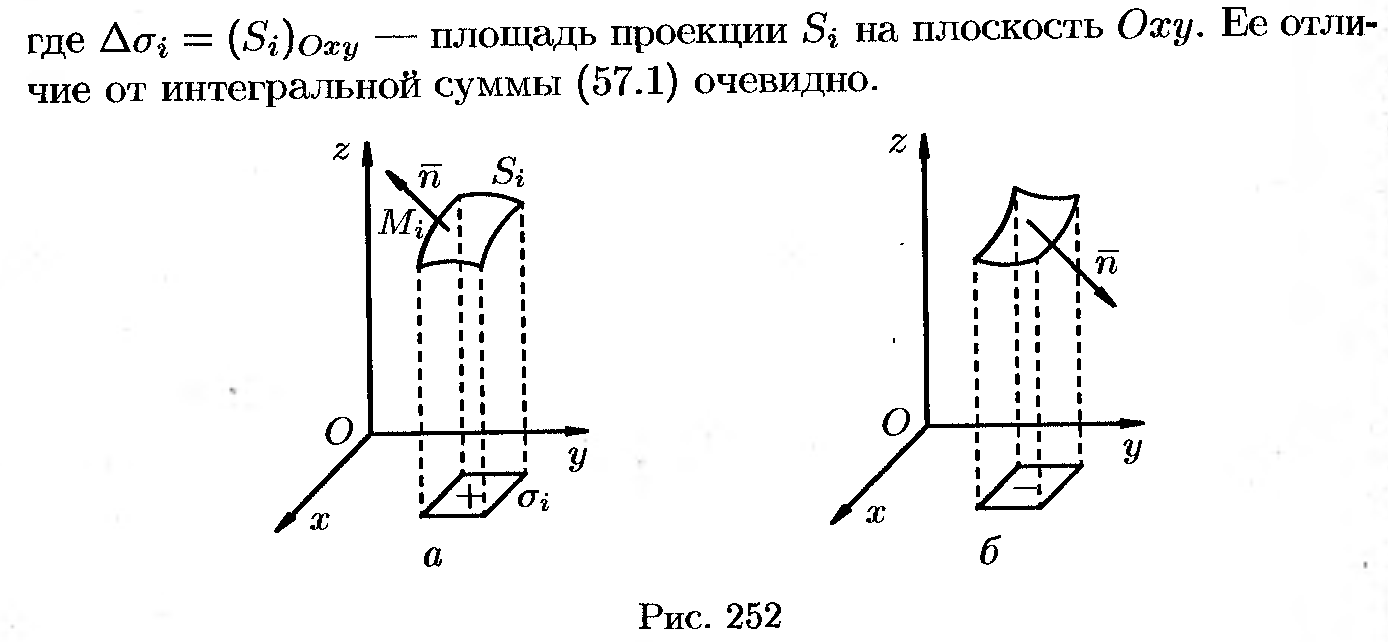
Пусть в точках рассматриваемой двусторонней поверхности S в пространстве Оxyz определена непрерывная функция f(x;y;z). выбранную поверхность разбиваем на части Si, где i=1,2,..., n и проектируем их на координатные плоскости. При этом площадь поверхности ∆σi берется со знаком плюс если выбрана верхняя сторона поверхности или что тоже самое если нормаль n к выбранной стороне поверхности составляет с осью Oz острый угол. В этом случае интегральная сумма имеет вид



















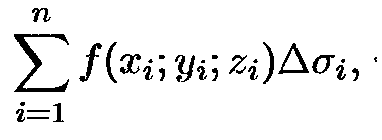
предел интегральной суммы при


если он существует и не зависит от способа разбиения поверхности S на части Si и от выбора точек
называется поверхностным интегралом второго рода от функции f(x;y;z) по переменным

х и у по выбранной стороне поверхности и обозначается






















































Вычисление поверхностного интеграла второго рода сводится к вычислению двойного интеграла.
Пусть функция R(x;y;z) непрерывна во всех точках поверхности S, заданной уравнением z=z(x,y), где z(x,y) — непрерывная функцияв замкнутой области D — проекции поверхности S на плоскость Oxy.
Выберем ту сторону поверхности S, где нормаль к ней образует с осью Oz острый угол. Тогда








правая часть этого равенства есть интегральная сумма для функции R(x;y;z(x,y)), непрерывной в области D. Переходя к пределу в равенстве (58.2) при λ → 0 получаем формулу




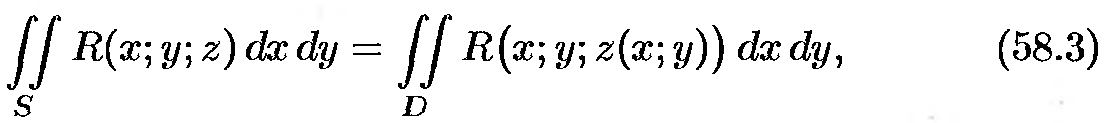
выражающую поверхностный интеграл второго рода по переменным х и у через двойной интеграл.
Если выбрать вторую сторону, т.е. Нижнюю, поверхности S, то полученный двойной интеграл будет со знаком минус.














Знаки перед интегралом выбираются в зависимости от ориентации поверхности S (так во второй формуле берем плюс если нормаль к поверхности образует с осью Оу острый угол, а знак минус — если тупой угол). Для вычисления общего поверхностного интеграла второго рода используют эти три формулы, проектируя поверхность S на все три координатные плоскости: