Формула Грина

связывает двойной интеграл по плоской области с криволинейным интегралом по контуру этой области.

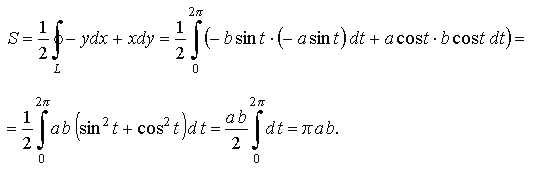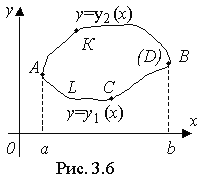
Пусть функции P(x,y), Q(x,y), P'_y(х,у), Q'_x(х,у) непрерывны в замкнутой области D, ограниченной контуром L (рис. 3.6).

Пусть контур L, кроме того, пересекается прямыми, параллельными осям координат, не более чем в двух точках.

Пусть уравнение АСВ есть y = y₁(x) при a ≤ x ≤ b , и уравнение АКВ есть y = y2(x) при a ≤ x ≤ b.

Преобразуем двойной интеграл:

здесь символ

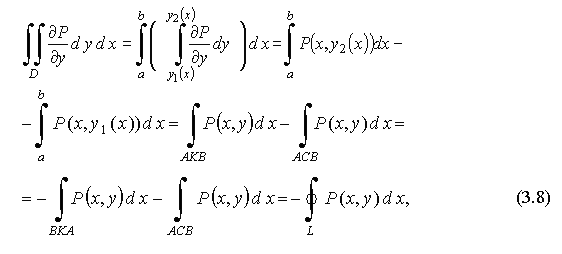
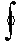означает криволинейный интеграл по замкнутому контуру L.

Аналогично получается

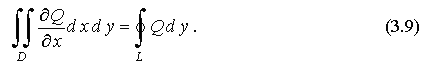
Вычитая из формулы (3.9) формулу (3.8), получаем формулу Грина

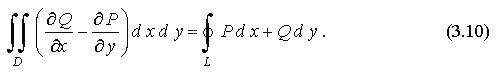
В формулах (3.8), (3.9) и (3.10) направление обхода контура - положительное (против часовой стрелки), т. е. область D при движении по контуру L всё время остается слева.

С помощью формулы Грина (3.10) можно получить выражения площади плоской фигуры через криволинейный интеграл по контуру этой фигуры.

Для этого достаточно подобрать P(x,y) и Q(х,y) такими, чтобы в области D выполнялось условие

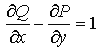
тогда двойной интеграл в формуле (3.10) будет давать величину S площади области D.

Например:

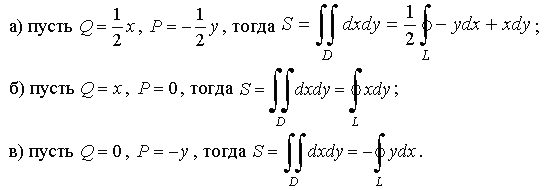
Пример 3.6. Вычислить площадь, ограниченную эллипсом: x=acost, y=bsint, 0≤ t ≤2π

Решение